编程の第一步：本屑最爱滴——列表！！！

由公式：

C(n, m) = (n!)/(m!*(n-m)!)

可手动计算出前几项的值。

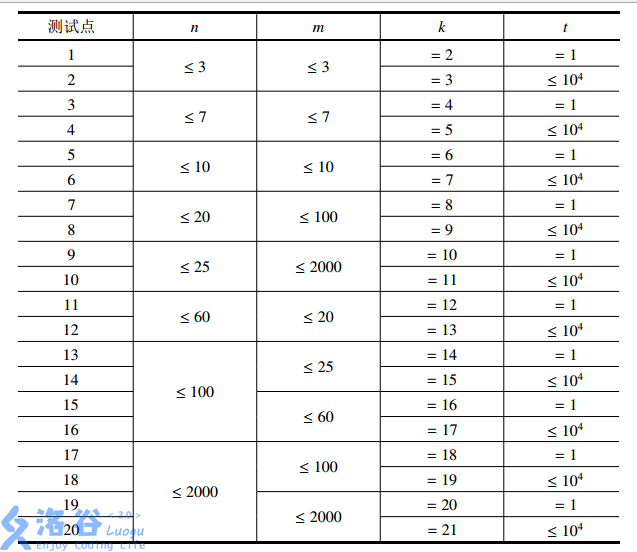
具体数据如下：

由于网站表格合并问题，部分数据后添加了“'”，请自行忽略

（情绪失控地）Ahahahahaaaa~~，费 递归 的OIer 100%警觉：杨辉三角！！！！！

于是乎，，

#include<cstdio>
#include<cmath>
using namespace std;

int k;  //存储 倍数，用于 取模运算
long long cyc[2001][2001];  //存储 杨辉三角

//初始化 杨辉三角
void set_up(){
    /* 杨辉三角 规律：
    ● cyc[i][0] = cyc[i][i] = 1    i ∈ N
    ● cyc[i][j] = cyc[i-1][j-1]+cyc[i-1][j]    i, j ∈ N* && j < i
    */

    cyc[0][0] = 1;
    
    for(int i=1; i<=2000; i++){
        cyc[i][0] = cyc[i][i] = 1;

        //优化：取模运算 (a+b)%k = (a%k+b%k)%k
        for(int j=1; j<i; j++) cyc[i][j] = (cyc[i-1][j-1]+cyc[i-1][j])%k;
    }

    return ;
}

int main(){
    int t;  //测试数据组数
    scanf("%d%d", &t, &k);
    
	set_up();  //初始化 杨辉三角

    while(t--){
        int n, m;
        scanf("%d%d", &n, &m);

        //查找 满足 C(i, j)%k==0 的 i, j 对数
        long long sum=0;
        for(int i=0; i<=n; i++){
            for(int j=0; j<=fmin(i, m); j++){
                if(cyc[i][j]%k == 0) sum++;
            }
        }

        printf("%lld\n", sum);
    }

    return 0;
}

写至此，信心满满地认为又双叒叕AC了一道氵题（尤其是取模优化后）。

WARNING：取模运算公式非常重要！！！

请务必牢记：(a+b)%k = (a%k+b%k)%k

Emmm…………

90 Time Exceeded

OK、OK！这lj题目是写不了一点儿！！！90？足矣！

🚀️ 写于 2023.11.6，状态：已完结

az... 好像看站外图片需要联网，看不鸟的，，奏当TA不存在罢。。()()

几个年后……

家银们，谁懂啊？！我AC了！！！！！（完了，它疯掉了>_<）

#include<cstdio>
#include<cmath>
using namespace std;

int k;  //存储 倍数，用于 取模运算
int n, m;  //C(n, m) = (n!)/(m!*(n-m)!)
long long cyc[2001][2001];  //存储 杨辉三角
long long ans[2001][2001];  //存储 遍历结果

/* ★ 全新优化：
使用数组存储遍历结果（ans[x][y] 表示 杨辉三角第 x 行到第 y 个数据时）满足 C(i, j)%k==0 的 i, j 对数
减小了程序时间复杂度【O(n^2) -> O(n)】，防止因重复遍历导致 TLE。。。
*/

//初始化 杨辉三角
void set_up(){
    /* 杨辉三角 规律：
    ● cyc[i][0] = cyc[i][i] = 1    i ∈ N
    ● cyc[i][j] = cyc[i-1][j-1]+cyc[i-1][j]    i, j ∈ N* && j < i
    */

    cyc[0][0] = 1;
    if(k == 1) ans[0][0] = 1;
    
    for(int i=1; i<=2000; i++){  
        long long c=0;  //存储 杨辉三角当前行到当前数据时满足 C(i, j)%k==0 的 i, j 对数

        cyc[i][0] = 1;
        if(k == 1) c++;

        ans[i][0] = c;

        //优化：取模运算 (a+b)%k = (a%k+b%k)%k
        for(int j=1; j<i; j++){
            cyc[i][j] = (cyc[i-1][j-1]+cyc[i-1][j])%k;
            if(cyc[i][j]%k == 0) c++;

            ans[i][j] = c;
        }

        cyc[i][i] = 1;
        if(k == 1) c++;
        
        ans[i][i] = c;
    }

    return ;
}

int main(){
    int t;  //测试数据组数
    scanf("%d%d", &t, &k);
    
	set_up();  //初始化 杨辉三角

    while(t--){
        scanf("%d%d", &n, &m);

        //查找 满足 C(i, j)%k==0 的 i, j 对数
        long long sum=0;
        for(int i=0; i<=n; i++) sum += ans[i][int(fmin(i, m))];

        printf("%lld\n", sum);
    }

    return 0;
}

100 Accepted

评测记录（尝试次数：∞）：❤️ 100 Accepted

🚀️ 写于 2023.11.16，状态：现在真的完结了~