2312wanghao

UID: 146, 注册于 2023-9-24 14:33:41, 最后登录于 2024-11-25 17:03:14, 目前离线.

解决了 212 道题目，RP: 237.78 (No. 18)

个人简介

wubba lubba dub dub！！.............................................

————退役————

QQ：3186217426 啥beyond玩意，根本不会写

//我的高精度加法
int hs(string a,string b)
{
string c;
int a1=a.size(),b1=b.size(),as[5001]={},bs[5001]={},nb[5001]={},slc;
for(int i=0;i<a1;i++)as[a1-i-1]=a[i]-'0';
for(int i=0;i<b1;i++)bs[b1-i-1]=b[i]-'0';
if(a1>b1)slc=a1;
else slc=b1;
for(int i=0;i<slc;i++)
{
nb[i]+=as[i]+bs[i];
nb[i+1]=nb[i]/10;
nb[i]%=10;
}
if(nb[slc])slc++;
for(int i=slc-1;i>=0;i--)
{
c+=nb[i]+'0';
}
h=s;
s=c;
}

快读模板

void read(long long &x){ 
    long long f=1;x=0;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
    while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
    x*=f;
}

Copy

~垃圾~排序

快速排序

int split(int l,int r){
    swap(a[l],a[(l+r)/2]);
    int t=a[l];//以中间作基准
    while(l<r){
        while(a[r]>t&&l<r)r--;//在左边找大的
        if(l<r)a[l++]=a[r];//大的换到右边
        while(a[l]<t&&l<r)l++;//在右边找小的
        if(l<r)a[r--]=a[l];//小的换到左边
    }
    a[l]=t;
    return l;
}
void q_sort(int l,int r){
    if(l>=r)return;
    int mid=split(l,r);
    q_sort(l,mid-1);
    q_sort(mid+1,r);
}

Copy

归并排序

void merge(int L1,int R1,int L2,int R2){
    int az=L1,bz=L2,cz=L1;
    int c[100010]={};
    while(az<=R1&&bz<=R2){
        if(a[az]>a[bz])c[cz++]=a[bz++];
        else c[cz++]=a[az++];
    }
    while(az<=R1)c[cz++]=a[az++];
    while(bz<=R2)c[cz++]=a[bz++];
    for(int i=L1;i<=R2;i++)a[i]=c[i];
}
void msort(int l,int r){
    if(l>=r)return;
    int mid=(l+r)/2;
    msort(l,mid);
    msort(mid+1,r);
    merge(l,mid,mid+1,r);
}

Copy

上二分学的~唯一有用的~东西：

lower_bound(首地址，尾地址，值);//第一个大于等于值的下标
upper_bound(首地址，尾地址，值);//第一个大于值的下标
nth_element(数组名,数组名+第k小元素,数组名+元素个数)

Copy

~每次都会写错~的双端队列和冲锋枪：

deque<int> dq;//声明一个队列dq，用于存储int型变量
    dq.push_front(x);//将表达式x的值插入队首 
    dq.push_back(x);//将表达式x的值插入队尾
    dq.pop_front();//弹出队首元素
    dq.pop_back();//弹出队尾元素
    dq.clear();//清空队列 
    x=dq.front();//获取队首元素的值，并赋值给x
    x=qu.back();//获取队尾元素的值，并赋值给x
    dq.empty();//判断队列dq是否为空，若为空则返回true
    dq.size();//返回队列dq中存储的元素的个数 

vector<int> v;  // 声明一个向量 v，用于存储 int 型变量
    v.push_back(x); // 将表达式 x 的值存入向量末尾
    v.pop_back();   // 删除向量的末尾元素
    x = v.front();  // 获取首元素的值，并赋给变量 x
    x = v.back();   // 获取尾元素的值，并赋给变量 x
    v.empty();      // 判断向量 v 是否为空，若为空则返回 true
    v.size();   // 返回向量 v 中存储的元素的个数
    v.clear();      // 清空向量

Copy

我最讨厌的高精（函数包装，复制即可食用）：

string add(string s1,string s2){//加法
    long long a[10010]={},b[10010]={},c[10010]={};
    long long la=s1.length(),lb=s2.length(),lc=max(la,lb),x=0;
    string ans="";
    for(int i=0;i<la;i++)a[i]=s1[la-i-1]-'0';
    for(int i=0;i<lb;i++)b[i]=s2[lb-i-1]-'0';
    for(int i=0;i<lc;i++){
        c[i]=a[i]+b[i]+x;
        x=c[i]/10;
        c[i]=c[i]%10;
    }
    if(x)c[lc++]=1;
    for(int i=lc-1;i>=0;i--)ans+=(c[i]+'0');
    return ans;
}
string sub(string s1,string s2){//减法
    long long a[10010]={},b[10010]={},c[10010]={};
    long long la=s1.length(),lb=s2.length(),lc=max(la,lb),x=0,f=0;
    string ans="";
    if((s1 < s2 && s1.length() == s2.length()) || s1.length() < s2.length()){
        f=1;
        string t=s1;
        s1=s2;
        s2=t;
        swap(la,lb);
        cout<<'-';
    }
    for(int i=0;i<la;i++)a[i]=s1[la-i-1]-'0';
    for(int i=0;i<lb;i++)b[i]=s2[lb-i-1]-'0';
    for(int i=0;i<lc;i++){
        c[i]=a[i]-b[i]-x;
        if(c[i]<0){
            x=1;
            c[i]+=10;
        }else x=0;
    }
    while(c[lc-1]==0&&lc>1)lc--;
    for(int i=lc-1;i>=0;i--)ans+=(c[i]+'0');
    return ans;
}
string mul(string s1,string s2){//乘法
    long long a[10010]={},b[10010]={},c[20010]={};
    long long la=s1.length();
    long long lb=s2.length();
    long long lc=la+lb;
    string ans="";
    for(int i=0;i<la;i++) a[i]=s1[la-1-i]-'0';
    for(int i=0;i<lb;i++) b[i]=s2[lb-1-i]-'0';
    for(int i=0;i<la;i++){ 
        for(int j=0;j<lb;j++){
            c[i+j]+=a[i]*b[j];
            c[i+j+1]+=c[i+j]/10;
            c[i+j]%=10;
        }
    }
    while(c[lc-1]==0&&lc>1){
        lc--;
    }
    for(int i=lc-1;i>=0;i--) ans+=(c[i]+'0');
    return ans;
}
string div(string s,int b){//高精除低精
    int n,a[101000],c[101000],la,lc;
    la=s.length(),lc=0;
    for(int i=0;i<la;i++)a[i]=s[i]-'0';
    long long x=0;
    string ans="";
    for(int i=0;i<la;i++){
        c[i]=(x*10+a[i])/b;
        x=(x*10+a[i])%b;
    }
    while(c[lc]==0&&lc+1<la) lc++;
    for(int i=lc;i<la;i++)ans+=(c[i]+'0');
    return ans;
}
//高精除高精忒麻烦了懒得写

Copy

七类~费脑子~的贪心(sort!)

1. 最优装载 (P2676)

2. 部分背包 (P2240)

3. 乘船问题 (P1094)

4. 交换类贪心 (P1080)

5. 不相交区间 (P1803)

6. 区间选点 (P1250)

7. 区间覆盖 (P1589)

~超级费脑子~的动态规划

重点：状态转移方程！

最长上升子序列方程：if(a[j]<a[i])dp[i]=max(dp[i],dp[j]+1)

最长公共子序列方程：if(a[i]==b[j])dp[i][j]=dp[i-1][j-1]+1,else dp[i][j]=max(dp[i-1][j],dp[i][j-1])

最大子段和方程：dp[i]=max(a[i],dp[i-1]+a[i])

~前缀差分懒得写~

补充：Dilworth 定理=最长上升的子序列的个数=最长不下降子序列的条数

背包

01背包模板：

//n=物品总数,c=背包容量,w[i]=第i个物品的重量,v[i]=第i个物品的价值 
    for(int i=1;i<=n;i++){//前i个物品 
        for(int j=c;j>=w[i];j--){//重量为j 
            dp[j]=max(dp[j],dp[j-w[i]]+v[i]);//dp[j](dp[i][j])=前i个物品背包重量为j的最大价值 
        }
    }

Copy

对于一个物品，只有选或不选两种情况不选就是前i-1个物品加起来的价值,那么就等于dpj，而选的话就是前i-1个物品加上第i个物品的价值, 那么就等于dp[j]+vi，但是在i-1个物品中背包重量为j的情况下背包可能被装满了,所以要牺牲w[i]的空间来装第i个物品,那么背包重量就得改成j-w[i],整个就是dp[j-w[i]]+vi，选或不选两种情况求个最大值就行了，所以状态转移方程就是dp[j]=max(dp[j],dp[j-w[i]]+v[i]) 而j的循环是倒着写的，是因为倒着写每一个重量不会被多次访问

完全背包模板：

for(int i=1;i<=n;i++){//前i个物品 
        for(int j=w[i];j<=c;j++){//重量为j 
            dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
    }

Copy

完全背包就是01背包的变形，你可以一直选这一个物品.既然可以一直选，那循环就要正着写，因为前面的状态可以被多次访问

多重背包模板：

for(int i=1;i<=n;i++){//前i种物品 
        for(int j=c;j>=w[i];j--){//重量为j 
            for(int k=0;k<=t[i]&&k*w[i]<=j;k++){//第i种物品选k个,t[i]表示第i种物品有几个 
                dp[j]=max(dp[j],dp[j-k*w[i]]+k*v[i]);
            }
        }
    }

Copy

多重背包也是01背包的变形，种选和不选两种情况变成了选几个，所以要用一个循环k来表示选几个

~巨恶心~的树

树的定义

树，是由n(n\ge0)n(n≥0)个结点构成的非线性，具有层次关系的有限集合。

当n=0n=0时，这棵树被称为空树。

当n\ne0n=0时，这棵树被称为非空树，有几个特点：

树中仅有一个被称为根的结点
除根节点外，其余结点可以划分成多个不相交子树

树的一些术语

子结点：对于某一个结点的子树的根叫做子节点
父结点：对于他的子节点来说叫做父节点
兄弟结点：具有相同父结点的结点互称为兄弟结点
结点的度：其子节点的个数
树的度：所有结点的度的最大值
叶结点：度为0的结点，也就是没有子节点的结点
分支结点：度不为0的结点，也就是有子节点的结点
结点层次：根结点在第一层，其他结点=其父结点+1
树的深度：所有结点的最大层数
结点高度：叶结点高度为1，其他节点=max(其所有子节点高度)+1
树的高度：等于根的高度
路径与路径长度：对于两个结点n和m之间所经过的结点称为结点n到m的路径，其长度为该路径包含的边的数量

~难上加难~的二叉树

性质

一棵二叉树第ii层的最大结点数为2^{i-1},i>12i−1**,i>**1
一颗深度为ii的最大结点总数为2^i-1,i>12i−1**,i>**1
对任何非空的二叉树，若n_0n0表示叶节点的个数，n_2n2是度为2的非叶节点的个数，那么两者满足关系：n_0=n_2+1n0=n2+1

遍历（dfs）

先序：根节点\to→左子树\to→右子树

code：

void dfs(int x){
    if(x==0)return;
    cout<<x<<" ";
    dfs(a[x].l);
    dfs(a[x].r);
}

Copy

中序：左子树\to→根节点\to→右子树

code：

void dfs(int x){
    if(x==0)return;
    dfs(a[x].l);
   cout<<x<<" ";
    dfs(a[x].r);
}

Copy

后序：左子树\to→右子树\to→根节点

code：

void dfs(int x){
    if(x==0)return;
    dfs(a[x].l);
    dfs(a[x].r);
   cout<<x<<" ";
}

Copy

二叉搜索树

定义：左子树<(\le)<(≤)根节点<(\le)<(≤)右子树

中序遍历二叉搜索树是非下降的

图（吐）论

图的定义

一个图G是一个二元组，即序偶<V,E>，或记作G=<V,E> ，其中V是有限非空集合，称为G的顶点集,V中的元素称为顶点或结点；E称为 G的边的集合，所有的边ei都属于E，都有v中的结点与之对应，称ei为 G的边。

图的基本概念/术语

无向图：每条边都是无向边的图。
有向图：每条边都是有向边的图。
平凡图：仅有一个结点而没有边构成的图。
自环：若一条边所关联的两个结点重合，则称此边为自环。
邻接：关联于同一条边的两个点和称为邻接的；关联于同一个点的两条边和是邻接的（或相邻的）。
路径:若顶点，则称从顶点vi0到vin存在一条路径。
路径长度：路径上的边数。
简单路径：若路径上的顶点除vi0和vin可以相同外，其它顶点都不相同。
回路或环：起点和终点相同的简单路径。
根：有向图中，若存在一顶点v，从该顶点有路径可以到图中其它所有顶点，则称此有向图为有根图，v 称为图的根。
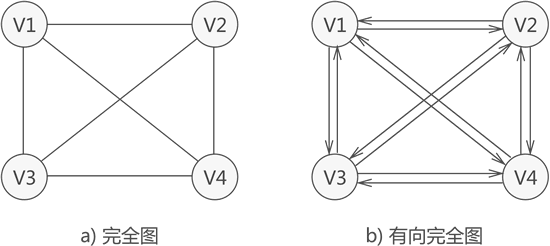
完全图：若图中各个顶点都与除自身外的其他顶点有关系，这样的无向图称为完全图（如图a)）。同时，满足此条件的有向图则称为有向完全图（图b)）。## 图的存储方式
邻接矩阵

一般用一个二维数组mp来存储

mp[i][j]表示i和j之间有没有边

//无向图
#include<bits/stdc++.h>
using namespace std;
int mp[1010][1010];
int n,m;
int main(){
    cin>>n>>m;
    for(int i=1;i<=m;i++){
        int x,y;
        cin>>x>>y;
        mp[x][y]=1;//x和y之间有一条边
        mp[y][x]=1;//无向图，反着再存
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            cout<<mp[i][j]<<" ";//如果i与j相邻，则输出1，否则输出0
        }
        cout<<endl;
    }
    return 0;
}

Copy

邻接表

一般用二维vector存储

v[x]存的是与x相邻的点

v[x][y]表示x与y相邻

邻接表可以方便求出每个点的出度

#include<bits/stdc++.h>
using namespace std;
vector<int>mp[1010];
int n,m,;
int main(){
    cin>>n>>m;
    for(int i=1;i<=m;i++){
        int x,y;
        cin>>x>>y;
        mp[x].push_back(y);//x与y之间有一条边，也就是x与y相邻
        mp[y].push_back(x);//无向图再反着存
    }
    for(int i=1;i<=n;i++){
        sort(mp[i].begin(),mp[i].end());
        cout<<mp[i].size()<<" ";//i的出度
        for(int j=0;j<mp[i].size();j++){
            cout<<mp[i][j]<<" ";//与i连接的点
        }
        cout<<endl;
    }

    return 0;
}//感谢"一行"大佬的逼急

1.数据类型：
(1)整数类：short;int;long;long long;  (unsigned)//希望有unsigned long long long long long long long......
    (2)浮点型：float;double;
    (3)其他类：bool;char;string;struct(用于定义数据类型);
2.变量(数组、函数、结构体等) 命名规则：
    (1)只能有字母、数字和_;
    (2)数字不能开头; 
    (3)名称严格区分大小写，且不能重复;
3.编程中的结构： 
    (1)顺序结构; //顺序结构yyds
    (2)分支结构:
        if(){       } else {        }
        switch(){       }
        ?: 
    (3)循环结构:
        while(){        }
        do{     }while()
        for(;;) {       }
    (4)循环跳转：
        break 从break语句开始，退出当前循环
        continue 从continue语句开始，跳过本次循环 
4.数组:一个存储多个数据的变量的集合。
    (1)数组下标：从0开始，到size()-1结束.
    (2)除char[]外，不能直接输入和输出 
    (3)初始化的方式a[]={0} ;
    (4)二维数组的定义:如果一维数组中的元素又是一个数组，先行后列。 
5.字符数组:char a[101] ;
    (1)求长度: strlen(a)
    (2)带空格的输入:cin.getline(a,101); 
    (3) 字符串连接:strcat(a,b);  将B连接在A的后面 
        字符串复制:strcpy(a,b);  将B复制给A
6.字符串string：string a; 
    (1)求长度: a.length(); 
    (2)带空格的输入:getline(cin,a);
    (3) 字符串连接:a+=b;  将B连接在A的后面 
        字符串复制:a=b;   将B复制给A
        字符串截取:s=s.substr(a,b) ;   从下标a开始截取b个字符
        字符串插入:s.insert(a,b) ;     在下标a前插入字符串b 
        字符串查找:s.find(a);   在字符串s中查找字符串a，找到返回第一位字符的下标， 
                                未找到返回unsigned long long的最大值 
7.函数:
    (1)包含：函数名、函数的参数及数据类型、函数的返回值类型(void)、函数体
    (2)常用函数:max(a,b);  min(a,b);  要求a,b数据类型相同 
                整数:abs(a);  浮点数:fabs(a);   数据类型区别 
                sqrt(a);   pow(a,b);   返回值为double类型 
                sort(a,a+n);   注意下标区别   
                swap(a,b);   无特殊要求。 
                memset(a,0,sizeof(a));   数组初始化
    (3)自定义函数:
        (1)质数判断:时间复杂度为 根号n。 
                int zs(int x){   if(x<=2) return 0;  for(int i=2;i*i<=x;i++) if(x%i==0) return 0; return 1;     }
        (2)数字翻转
                int fz(int x){   int a=0;  while(x) { a=a*10+x%10; x/=10;   }  return a;}
        (3)进制转换 (十进制转二进制：递归实现) 
                void zh(int x) {    if(x==0) return ;  zh(x/2);  cout<<x%2; }
        (4)递归 (fib)
                int fib(int x){   if(x<=2) return 1;   return fib(x-1)+fib(x-2);    }
8.进制转换与原反补码
    (1)进制转换：模除法。
    (2)特殊的进制转换：
        (1)二进制与八进制:
            二转八：二进制从最低位开始每3位转换为一个八进制的1位，顺序书写即可。 
            八转二： 八进制的每位转换成一个3位的二进制数，顺序书写即可。 
        (2)二进制与十六进制:
            二转十六：二进制从最低位开始每4位转换为一个十六进制的1位，顺序书写即可。 
            十六转二：十六进制的每位转换成一个4位的二进制数，顺序书写即可。 
    (3) 原码：用最高位表示数字的符号，0为正数，1为负数
        反码：正数不变，负数除符号位外，全部取反
        补码：正数不变，负数为反码+1
9.运算优先级
() 大于! ++ -- 大于 * / % 大于 + - 大于 >> << 大于  > >= < <= 
大于 == != 大于 && 大于 || 大于 = += -=... 
10.输入与输出
    (1)cin 与 cout  iostream 
    (2)scanf 与 printf  cstdio
    (3)速度:scanf/printf快于cin/cout    '\n'快于endl
    (4) %d-int/bool   %f-float  %lf-double %lld-long long  %c-char  %s-char[] 
        %u-unsigned int  %llu-unsigned long long   
        %5d-整数至少5位场宽，右对齐   %-5d-整数至少5位场宽，左对齐
        %5s-字符串场宽至少为5，右对齐 %-5s-字符串场宽至少为5，左对齐   
        %5.3s-字符串从右往左截取3位，场宽5，右对齐  %-5.3s-字符串从右往左截取3位，场宽5，左对齐 
        %5.3lf-保留3位，场宽5，右对齐  %-5.3lf-保留3位，场宽5，左对齐
        iomanip   cout<<fixed<<setprecision(3)<<a;   保留3位小数
11.位运算： 
    (1) &   二进制中，有0则为0 。  if(x%2==1)相当于 if(x&1==1) 
    (2) |   二进制中，有1则为1 。 
    (3) ^   二进制中，相同为0，不同为1 。a^a=0  a^0=a   
    (4) ~   ~a=-a-1 
    (5) >>  a>>=1相当于a/=2 
    (6) <<  a<<=1相当于a*=2     
12.排序：
    (1)冒泡：for(i 表示轮) for(j 表示下标)  比较与交换 
    (2)选择：for(i 表示轮) 找最小(大)值， 与第i个进行交换
    (3)插入：for(i 表示轮) 把当前元素依次向前对比和交换，比其小则停止
    (4)桶排：用数组下标进行排序的方式
    (5)快排：sort(a,a+n)   
    (6)结构体排序：使用struct 和 sort进行排序，需要自定义cmp函数 
13.高精度：
    (1)加法和减法:用数组的每一位存数字的每一位。
    (2)步骤:  存储-转换-计算-特判-输出
14.递推与递归：
    (1)递推用循环、递归用函数
    (2)递推关系与初始条件 
15.文件流//真的？
    (1) freopen("1.in","r",stdin);
    (2) freopen("1.out","w",stdout);

感谢不知名大佬的逼急

朴素简便的u盘插入方法（截止2024年仍可用）

1.把优盘变成pe盘 2.插上优盘重新开机 3.按f9 管理员密码是一个和安阳一中非常贴近的密码 4.打开你u盘中的pe系统 5.u盘启动！！

朴素简便的关机方法

用于你亲爱的朋友 1.win+m alt+F4 回车 2.win+x u u ~~快去关爱一下你的好朋友吧~~

更加朴素简便的关机方法

~~拔网线~~

€‘‚ƒ„…†‡ˆ‰Š‹ŒŽ‘’“”•–—˜™š››œžŸ ¡¢£¤¥¦§¨©ª«¬®¯°±²³´µ¶·¸¹º»¼½¾¿ÀÁÂÃÄÅÆÇÈÉÊËÌÍÎÏÐÑÒÓÔÕÖ×ØÙÚÛÜÝÞßàáâãäåæçèéêëìíîïðñòóôõö÷øùúûüýþÿ

————退役————

通过的题目
P01

P02

P03

P20

P23

P36

P43

P103

P107

P110

P115

P119

P126

P131

P135

P138

P139

P140

P142

P146

P147

P155

P179

P197

P207

P214

P227

P228

P247

P257

P261

P277

P301

P302

P303

P304

P305

P306

P307

P308

P309

P310

P311

P312

P313

P314

P315

P316

P317

P318

P319

P320

P321
P322

P323

P324

P327

P328

P329

P330

P331

P332

P333

P334

P335

P338

P339

P341

P342

P343

P344

P346

P347

P348

P349

P350

P352

P353

P354

P355

P356

P357

P358

P359

P360

P361

P362

P363

P364

P365

P366

P367

P368

P369

P370

P371

P372

P373

P376

P378

P379

P380

P381

P382

P384

P385
P386

P387

P389

P390

P391

P392

P393

P394

P395

P396

P397

P398

P399

P401

P403

P407

P410

P411

P412

P413

P414

P415

P416

P419

P421

P423

P424

P425

P430

P431

P437

P454

P455

P462

P463

P464

P470

P476

P477

P484

P488

P490

P491

P493

P494

P495

P519

P521

P528

P531

P532

P558

P578
P688

P700

P701

P703

P722

P724

P730

P742

P755

P756

P884

P899

P900

P992

P1305

P1312

P1323

P1326

P1330

P1345

P1349

P1498

P1548

P1552

P1566

P1571

P1617

P1633

P1634

P1635

P1636

P1638

P1639

P1680

P1756

P1757

P1776

P1784

P1960

P1999

P2002

P2024

P2099

P2108

P2113

P2117

P2121

P2135

P2141

P2143

P2144

P2145

P2154
最近活动
最近编写的题解
计数问题（count）

求s=1+2+...+n（jia）

基础算法: 33
课课通: 24
动态规划: 23
数组: 20
普及组: 19
模拟: 17
其他: 13
字符串: 10
数据结构: 8
高精度: 7
搜索: 7
提高组: 7
排序: 7
函数: 7
基础数据结构: 7
图结构: 6
贪心: 6
背包: 6
USACO: 5
递推: 5

2312wanghao

个人简介

wubba lubba dub dub！！.............................................

————退役————

快读模板

~垃圾~排序

快速排序

归并排序

上二分学的~唯一有用的~东西：

~每次都会写错~的双端队列和冲锋枪：

我最讨厌的高精（函数包装，复制即可食用）：

七类~费脑子~的贪心(sort!)

1. 最优装载 (P2676)

2. 部分背包 (P2240)

3. 乘船问题 (P1094)

4. 交换类贪心 (P1080)

5. 不相交区间 (P1803)

6. 区间选点 (P1250)

7. 区间覆盖 (P1589)

~超级费脑子~的动态规划

重点：状态转移方程！

最长上升子序列方程：if(a[j]<a[i])dp[i]=max(dp[i],dp[j]+1)

最长公共子序列方程：if(a[i]==b[j])dp[i][j]=dp[i-1][j-1]+1,else dp[i][j]=max(dp[i-1][j],dp[i][j-1])

最大子段和方程：dp[i]=max(a[i],dp[i-1]+a[i])

~前缀差分懒得写~

背包

01背包模板：

完全背包模板：

多重背包模板：

~巨恶心~的树

树的定义

树的一些术语

~难上加难~的二叉树

性质

遍历（dfs）

先序：根节点\to​→​左子树\to​→​右子树

code：

中序：左子树\to​→​根节点\to​→​右子树

code：

后序：左子树\to​→​右子树\to​→​根节点

code：

二叉搜索树

定义：左子树<(\le)​**<​(​≤​)根节点<(\le)​<​(​≤**​)右子树

中序遍历二叉搜索树是非下降的

图（吐）论

图的定义

图的基本概念/术语

邻接矩阵

邻接表

朴素简便的u盘插入方法（截止2024年仍可用）

朴素简便的关机方法

更加朴素简便的关机方法

————退役————

通过的题目

最近活动

最近编写的题解

题目标签

状态

开发

支持

登录

先序：根节点\to→左子树\to→右子树

中序：左子树\to→根节点\to→右子树

后序：左子树\to→右子树\to→根节点

定义：左子树<(\le)<(≤)根节点<(\le)<(≤)右子树